La Figura 1 è una foto del mio globo celeste sulla quale ho indicato i principali elementi che sono presenti. Il globo vero e proprio, del diametro di 30cm (Edizioni Nova Rico Firenze 1978) l’avevo acquistato nei primi anni ’90. Era montato sullo stesso supporto inclinato del mappamondo (23½° come l’asse terrestre) ed aveva una lampada interna che da accesa evidenziava le figure mitologiche sulle relative costellazioni.
Per il globo celeste il supporto inclinato del mappamondo è una soluzione di comodo ed estetica, ma dal punto di vista astronomico non ha senso. Esiste però un’altra soluzione bella esteticamente e soprattutto azzeccata dal punto di vista astronomico: la montatura classica ad anello inserita nel piano orizzontale o piano locale. Nei secoli passati non a caso i globi celesti venivano realizzati con questa montatura (Figura 1bis).

Ci ho pensato un po’ a come potevo fare e poi mi sono deciso a realizzarla. Alla fine di questo non facile lavoro il mio globo celeste era diventato proprio come volevo. Facendo alcune prove mi sono reso conto che dal punto di vista didattico e divulgativo è il massimo che si può avere. In primo luogo per i seguenti motivi:
è il modello meccanico del cielo più semplice e intuitivo
riproduce il cielo per qualsiasi località della Terra, e per qualsiasi data e ora
si può sperimentare personalmente a piacimento
(Riguardo al secondo punto c’è da dire che la cartografia del globo andrebbe aggiornata ogni 50 anni a causa della precessione degli equinozi che, rispetto alle stelle, fa slittare di circa 1,4° al secolo il punto gamma insieme alle coordinate equatoriali ed eclittiche.)
I produttori purtroppo continuano a mettere il globo celeste sullo stesso supporto inclinato del mappamondo, evidentemente a loro basta solo che sia un bell’oggetto, anche se nella sostanza è stupido e inutile: un regalo per un bambino che poi non saprà cosa farsene, o un soprammobile un po’ chic. Devo dire purtroppo anche per il mondo della scuola e per il mondo della divulgazione che hanno sempre ignorato il globo celeste. Possiamo solo sperare che una buona volta chi di dovere prenda in seria considerazione il globo celeste per il ruolo didattico e divulgativo che può avere.
Vediamo il mio globo celeste nella Figura 1, nel disegno schematico della Figura 2 e per alcuni dettagli nelle due figure successive.
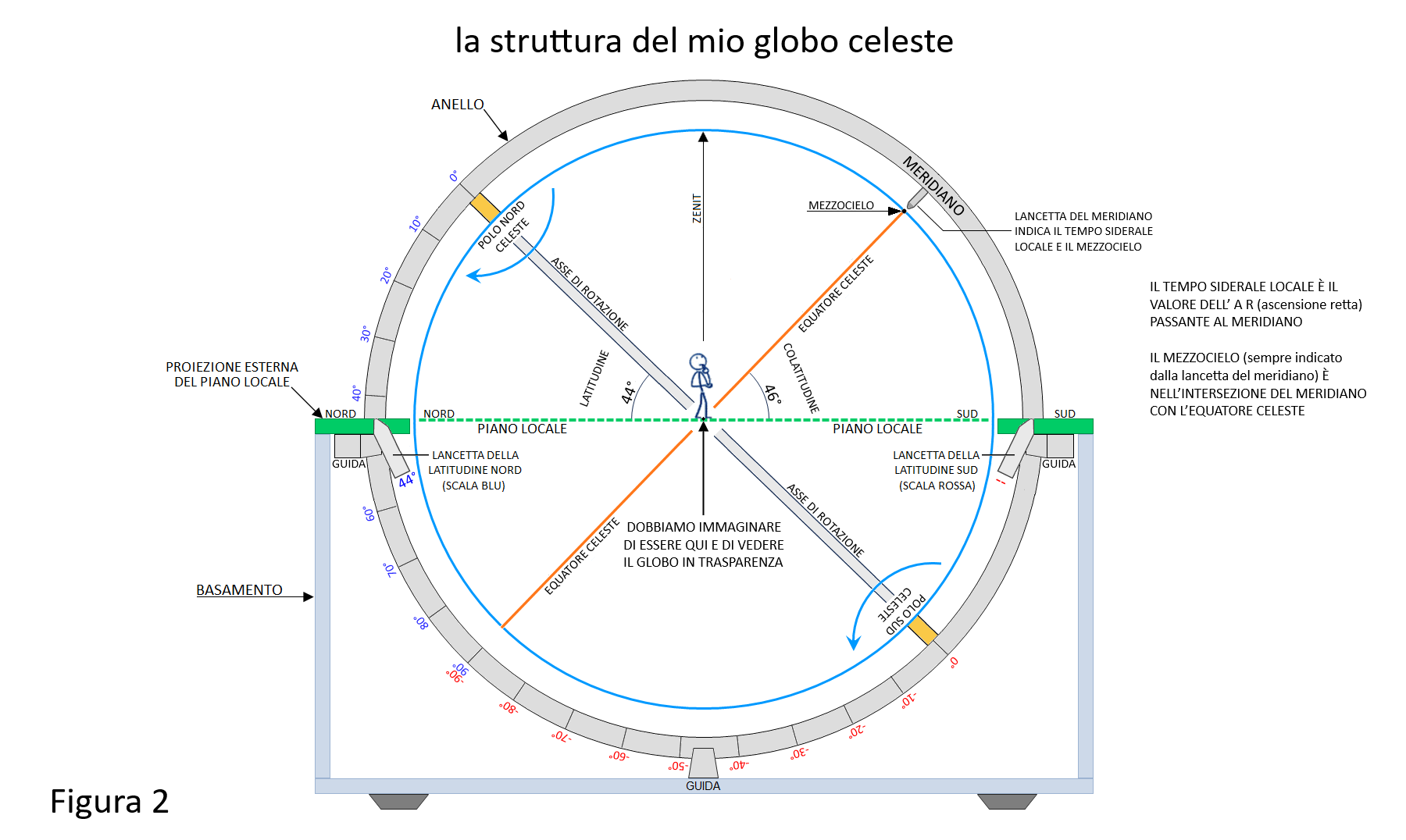
Il globo celeste riproduce la rotazione della sfera celeste, e quindi di tutti gli elementi geometrici e fisici che essa supporta, intorno al nostro piano locale (vedi Figura 1). Non solo intorno al nostro piano locale, ma anche intorno al piano locale di qualsiasi altro luogo della Terra.
Per piano locale intendo il piano tangente alla sfera terrestre nel punto dove si trova la località. Il piano locale di Forlì ad esempio è il piano tangente alla sfera terrestre nel punto dove si trova Forlì, latitudine 44° Nord e longitudine 12° Est di Greenwich (valori arrotondati). Ogni piano locale avrà un suo punto di tangenza sulla sfera terrestre e quindi anche un suo orientamento rispetto sia alla sfera terrestre che alla sfera celeste. Per ogni piano locale la direzione Nord-Sud è lungo il suo meridiano locale (Nord verso il Polo Nord e Sud verso il Polo Sud) e la direzione Est-Ovest è lungo il suo parallelo locale (guardando a Sud a sinistra c’è l’Est e a destra c’è l’Ovest).
Possiamo riprodurre il cielo di qualsiasi luogo per qualsiasi data e ora agendo semplicemente su due regolazioni tra loro perpendicolari:
1) la latitudine locale, si imposta ruotando l’anello
2) il tempo siderale locale, si mette a punto ruotando il globo
Guardiamo ancora la Figura 1. Per impostare la latitudine locale si devono contare le tacche: i tre punti sono le decine, i due punti il 5 (unità intermedia) e i punti singoli le altre unità. Per Forlì basta portare il Polo Nord celeste 44° sopra la direzione Nord del piano locale servendosi dell’apposita lancetta.
Sempre nella Figura 1 vediamo che l’equatore del globo è suddiviso in 24 ore di AR (abbreviazione di ascensione retta) suddivise in 6 parti di 10 minuti. Fissata sull’anello in alto a destra c’è la lancetta del meridiano che indica oltre al mezzocielo (l’intersezione del meridiano locale, rappresentato dall’anello, con l’equatore celeste) anche il tempo siderale locale sull’equatore del globo, cioè l’ora di AR passante al meridiano. Il tempo siderale locale dipende dalla data, dall’ora e dalla longitudine locale. Lo si può determinare in diversi modi: con un software astronomico, calcolandolo con l’apposita formula, ed anche con un semplice regolo circolare chiamato “orologio siderale”. Quest’ultimo si coniuga perfettamente con il globo celeste. È l’oggetto del secondo articolo della scheda dei modelli astronomici nel quale spiego la differenza tra il tempo solare o civile e il tempo siderale. Qui ci basta sapere che il tempo solare o civile fa riferimento al Sole che sulla sfera celeste si sposta di circa 1° al giorno, mentre il tempo siderale locale fa riferimento al punto gamma (Figura 3) che sulla sfera celeste è fisso, in pratica è l’ora di AR passante al meridiano. Nel modello il suo valore è indicato bene dalla lancetta del meridiano.

Nella realizzazione artigianale della montatura ho incontrato qualche difficoltà, ma grazie anche ad un po’ di fortuna che mi ha assistito alla fine sono rimasto molto soddisfatto del risultato. Non ho fatto tutto da solo ma ho potuto contare sull’aiuto di un bravo fabbro che ha fatto l’anello di ferro (era il pezzo che mi preoccupava di più), con una calandra (macchina utensile che attraverso dei rulli regolabili imprime una curvatura uniforme ad una barra di ferro); di un tornitore che ha fatto l’asse di rotazione (inteso fisicamente), i due tappi e i due distanziatori; di mio babbo che ha verniciato a spruzzo i pezzi del basamento in legno compensato.
Possiamo dividere il globo celeste in due parti, una parte fissa e una parte mobile. La parte fissa è costituita dal basamento, nel mio una scatola di legno compensato a forma di prisma ottagonale. Le facce laterali sono 4, una sì e una no alternate, ma bastano a conferire rigidità al basamento. La base superiore al suo centro ha un ampio buco circolare del diametro di 31cm e due gole, una a Nord e l’altra a Sud, per ospitare il globo (diametro 30cm) e l’anello (diametro esterno 35,4cm, spessore 12mm).
All’interno del basamento ci sono le 3 guide dell’anello, una inferiore centrale sulla base inferiore e due laterali sotto le due gole della base superiore una a Nord e l’altra a Sud. Queste 3 guide vincolano l’anello nella posizione precisa che deve sempre mantenere: sulla linea Nord-Sud, perpendicolare al piano locale, esattamente metà sopra e metà sotto di esso affinché il piano locale passi per il centro del globo. Si può ruotare l’anello facendolo scorrere nelle guide per impostare la latitudine locale.
La superficie verde, il sopra della base superiore, rappresenta il piano locale dell’osservatore o meglio la sua proiezione esterna al globo con le targhette dei 4 punti cardinali e dei 4 punti intermedi. Vicino al bordo interno ci sono 36 piolini ogni 10° di azimut, in realtà 34 perché ne manca uno nella gola Nord e uno nella gola Sud. Nel modello noi come ipotetici osservatori ci dobbiamo collocare idealmente sul piano locale e al centro del globo dove si incrociano le rette Nord-Sud ed Est-Ovest (vedi Figura 2). Da lì immaginiamo di osservare il globo in trasparenza. Visto da fuori il globo è invertito in senso orizzontale, cioè destra ↔ sinistra (come una scritta sul vetro appannato delle finestre di una volta letta dall’altra parte). Per non confonderci dobbiamo fare riferimento ai punti cardinali che ci riportano intuitivamente al centro del globo.
Infine ci sono le due lancette con la punta sagomata radente al piano, una sulla gola Nord per indicare la latitudine Nord sul fianco graduato dell’anello, l’altra sulla gola Sud per indicare la latitudine Sud sul fianco graduato dell’anello. Sulla gola Sud la parte graduata dell’anello compare solo quando ruotando l’anello facciamo salire il Polo Sud celeste sopra il piano locale dalla gola Sud. Dalla gola Nord devono salire solo le gradazioni delle latitudini Nord e dalla gola Sud devono salire solo le gradazioni delle latitudini Sud.
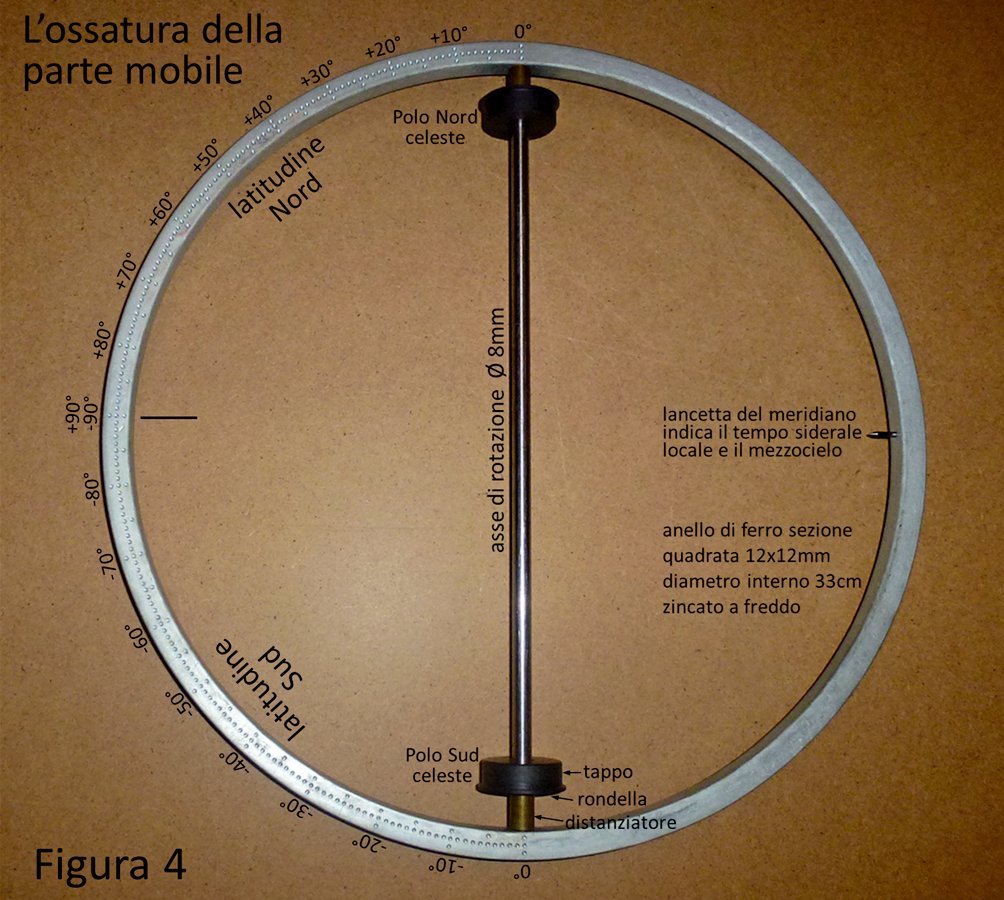
La parte mobile è costituita dall’anello, dall’asse di rotazione e dal globo. L’anello ha la forma circolare. Il centro dell’anello coincide con il centro del globo e questo, anche ruotando l’anello, giace sempre sul piano locale al centro dei punti cardinali, l’incrocio delle rette Nord-Sud ed Est-Ovest. La Figura 4 mostra l’ossatura della parte mobile (senza il globo). L’asse di rotazione è fissato diametralmente nell’anello con due viti M3 a testa svasata che scompare sotto la superficie dell’anello.
I due tappi in PVC sono forati centralmente Ø 8mm per ruotare centrati sull’asse di rotazione, mentre esternamente entrano stretti nei buchi polari del globo che viene vincolato a sua volta a ruotare centrato sull’asse di rotazione. I due distanziatori (ricavati da un tubino di ottone Ø interno 8mm Ø esterno 10mm) sono della stessa altezza così centrano il globo lungo l’asse e quindi anche nell’anello (tra i distanziatori e i tappi in PVC ho interposto una rondella di acciaio inox 6x18 ripassata Ø 8mm, perché la rondella da 8mm ballava un po’). Nella Figura 4 vediamo come vanno letti i valori della latitudine nella parte graduata.
I passi della sequenza da 1 a 6 spiegano geometricamente in pochi passaggi come partendo dal piano locale si arriva al globo celeste. Seguiamo attentamente questi 6 passi.
Il Sole è il protagonista principale del cielo, quello che quando è sopra il piano locale fa il cielo diurno, mentre quando è sotto il piano locale dà spazio al cielo notturno (a parte i crepuscoli serale e mattutino). L’eclittica è il percorso (apparente) annuale che il Sole fa sulla sfera celeste. Nella Figura 1 l’eclittica è quella linea graduata dove le tacche distano tra loro circa 1° e indicano la posizione del Sole nei 365 giorni dell’anno. Per capire perché vediamo il Sole percorrere l’eclittica col passo di circa 1° al giorno guardiamo la Figura 5.
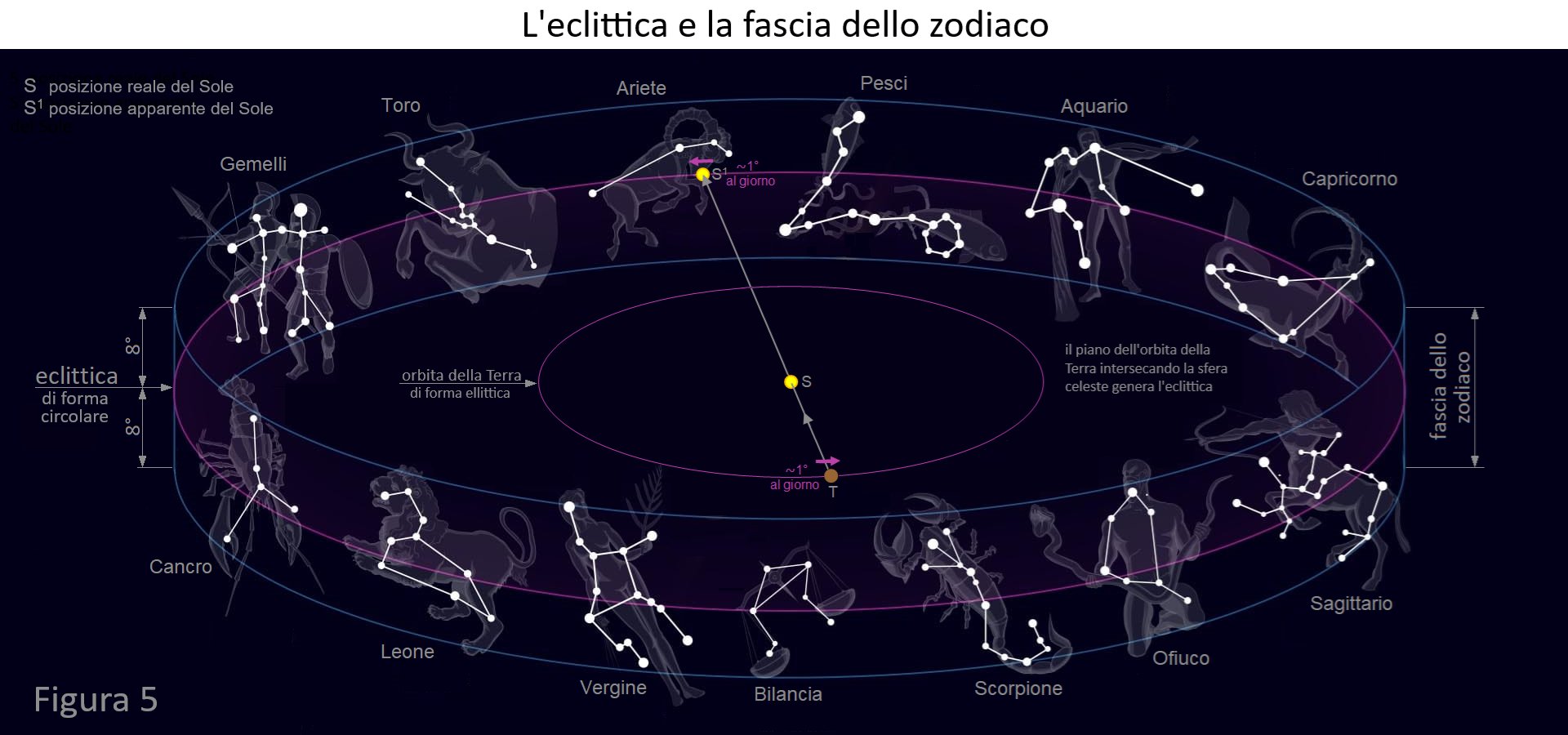
Al centro abbiamo il Sole S e la Terra T che gli ruota intono lungo la sua orbita ellittica (rivoluzione). Il piano dell’orbita della Terra è passante per il centro del Sole. Prolunghiamo questo piano fino a intersecare la sfera celeste: la linea di intersezione è l’eclittica che però non è ellittica come l’orbita della Terra, ma circolare perché è una sezione della sfera celeste.
La Terra è in T e il Sole in S, quindi vediamo il Sole in direzione T→S.
Noi percepiamo visivamente le dimensioni del Sole, possiamo misurare il suo diametro angolare e troviamo che è 0,53°, come una moneta da 1Euro a 2,5 metri dal nostro occhio che copre esattamente il disco solare (esperimento da non fare senza un filtro adeguato perché guardare direttamente il Sole danneggia gravemente la vista), ma la sua distanza non la possiamo percepire. Il Sole così lo vediamo del suo diametro angolare di 0,53° ma proiettato in S1 sull’eclittica.
La Terra percorre i 360° della sua orbita in 365,25giorni, quindi circa 1° al giorno (mediamente 0,9856°). Di conseguenza in direzione opposta osserviamo il Sole percorrere l’eclittica con lo stesso passo. C’è una cosa importante da dire: la sfera celeste è praticamente infinita per cui l’orbita della Terra al suo confronto è praticamente puntiforme, quindi la parte centrale della Figura 5 con il Sole e la Terra che percorre la sua orbita la dobbiamo immaginare concentrata in un punto. Altrimenti vedremmo le costellazioni più grandi o più piccole a seconda della nostra posizione nell’orbita, mentre durante l’anno le vediamo sempre esattamente delle stesse dimensioni.
L’equatore celeste e l’eclittica sono cerchi massimi della sfera celeste essendo originati da piani che passano per il centro della sfera celeste. L’eclittica è centrale nella fascia dello zodiaco larga 8° sopra e 8° sotto di essa. La Luna e i pianeti li vediamo tutti proiettati sulla fascia dello zodiaco e nel tempo si muovono più o meno velocemente dentro questa fascia. Questo perché il Sistema solare è abbastanza piatto, e dal nostro punto di vista la sua proiezione sulla sfera celeste finisce all’interno della fascia dello zodiaco.
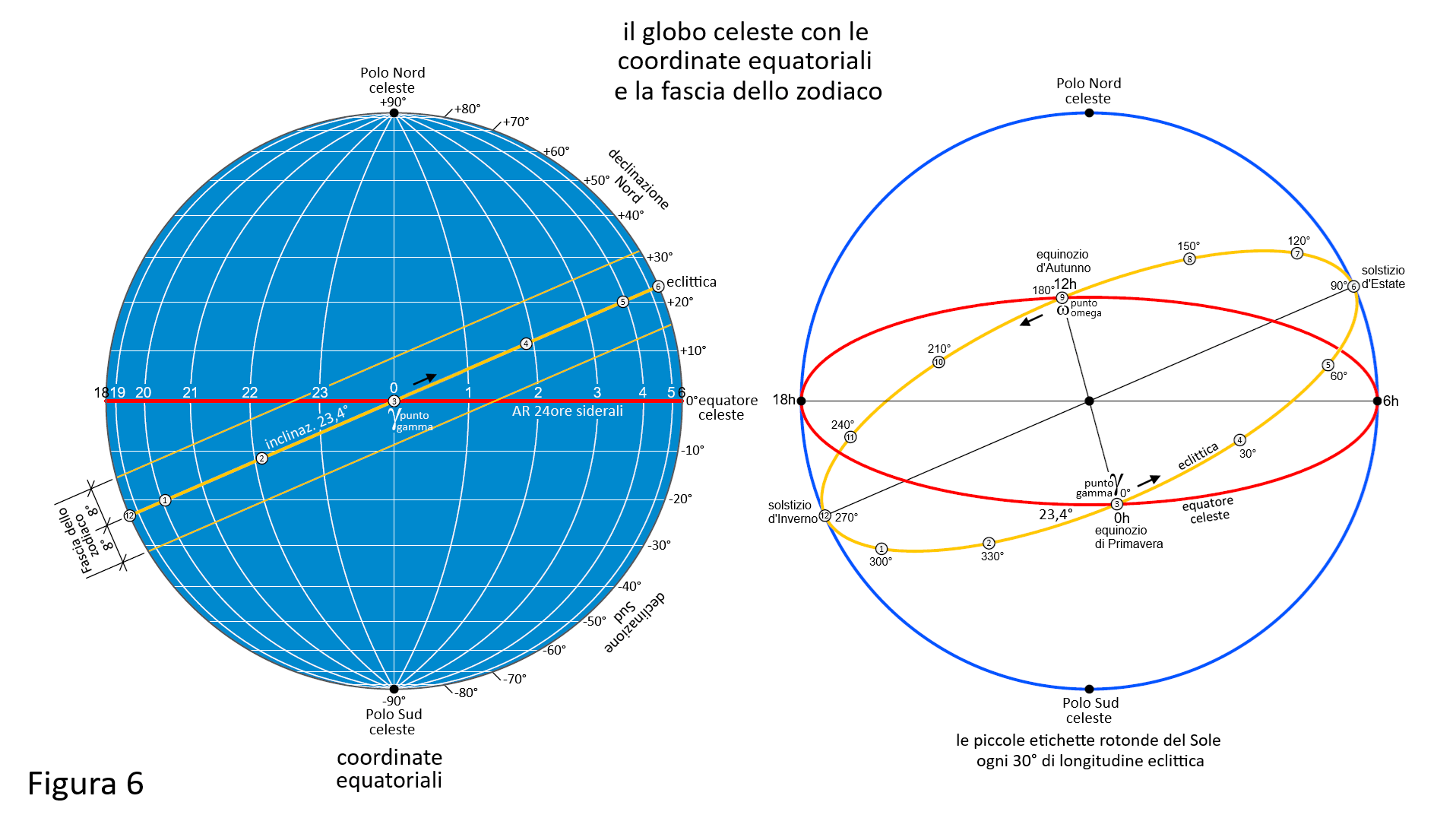
Vediamo ora la sfera celeste con i suoi due principali sistemi di riferimento che hanno come origine o lo zero il punto gamma:
Le coordinate equatoriali:
AR (ascensione retta) suddivisa in 24 ore siderali
Declinazione da 0° a +90° Nord da 0° a -90° Sud
Sono analoghe alle coordinate terrestri: l’AR alla longitudine e la declinazione alla latitudine.
Le coordinate eclittiche si usano normalmente nella fascia dello zodiaco anche se si possono estendere a tutta la sfera celeste:
Longitudine eclittica da 0° a 360° a partire dal punto gamma
Latitudine eclittica da 0° a +90° Nord eclittico e da 0° a -90° Sud eclittico
L’eclittica e la fascia dello zodiaco sono inclinate di 23,4° rispetto all’equatore celeste. Il punto dove l’eclittica interseca l’equatore celeste nell’equinozio di Primavera, quindi dal basso verso l’alto, è il punto gamma, principale punto di riferimento della sfera celeste (AR 0ore, longitudine eclittica 0°).
Lungo l’eclittica ho apposto delle piccole etichette tonde (Ø 8mm) con i numeri dei mesi da 1 a 12 che rappresentano il Sole nei 12 punti cardinali dell’eclittica (longitudine eclittica 0° - 30° - 60° - 90° - 120° - 150° - 180° - 210° - 240° - 270° - 300° - 330°). Sono posizionate intorno al 20-21 di ogni mese, quelle di marzo ③ e di settembre ⑨ coincidono con gli equinozi (longitudine eclittica 0° e 180°), quelle di giugno ⑥ e di dicembre ⑫ con i solstizi (longitudine eclittica 90° e 270°). Convenzionalmente sono i confini dei segni zodiacali.
Il diametro apparente del Sole come abbiamo detto è 0,53°, ma sul globo che diametro in mm dovrebbe il Sole? Il diametro del globo è 30cm e quindi la sua circonferenza è 94,2cm (30 x 3,14 = 94,2); 360° corrispondono a 94,2cm quindi 1° corrisponde a 94,2cm / 360 = 2,6mm. Sul globo il Sole avrebbe un diametro di 2,6mm x 0,53 = 1,4mm, più piccolo della sezione di un comune stuzzicadenti (Ø 2mm). Quindi teniamo presente che il Sole in realtà sarebbe molto più piccolo delle etichette che lo rappresentano.
Nella Tabella 1 possiamo vedere i dati relativi alle 12 etichette situate sui 12 punti cardinali dell’eclittica. Vediamoli insieme alla Figura 6.
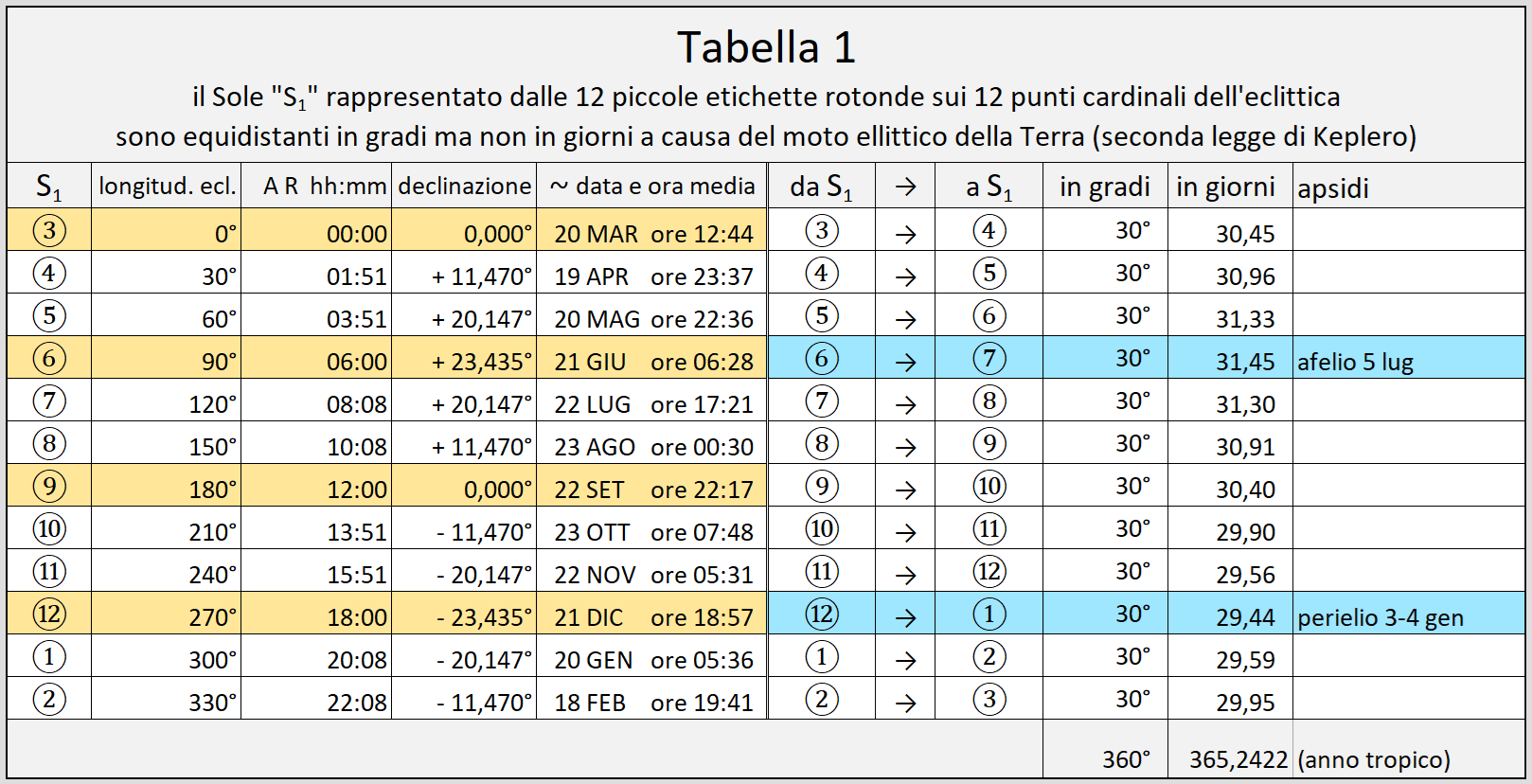
Abbiamo la longitudine eclittica in gradi; l’ascensione retta AR in ore e minuti; la declinazione in gradi; la data e ora media del passaggio del Sole in questi 12 punti cardinali (nel ciclo di quattro anni comprendenti l’anno bisestile oscilla fino a circa 8h 40m prima e dopo); la distanza in gradi lungo l’eclittica tra un punto e l’altro che è sempre di 30°; per la seconda legge di Keplero la stessa distanza in giorni varia dai 29,44 giorni nel tratto che comprende il perielio, ai 31,45 giorni nel tratto che comprendere l’afelio. La somma di questi tratti in giorni è di 365,2422 giorni che è la durata dell’anno tropico corrispondente all’intervallo tra due passaggi successivi del Sole all’equinozio di Primavera. Il nostro anno civile, con gli aggiustamenti del calendario gregoriano disposti su un ciclo di 400 anni, si mantiene allineato all’anno tropico. Seguendo la regola di questi aggiustamenti negli anni di fine secolo non divisibili per 400, quindi il 1700, il 1800 e il 1900 è stato eliminato il 29 febbraio, mentre in quelli divisibili per 400, quindi il 1600 e il 2000 è rimasto il 29 febbraio. Nel 2100 verrà eliminato il 29 febbraio.
Vediamo come cambia l’aspetto del cielo serale mese dopo mese cominciando dall’equinozio di Primavera. Facciamo tramontare l’etichetta ③ a Ovest e poi facciamo avanzare il tempo siderale di almeno un’ora per far passare completamente il crepuscolo: abbiamo così l’aspetto del cielo del 20 marzo dopo che ha fatto buio. Facciamo la stessa cosa con la ④, la ⑤, la ⑥… Mese dopo mese avremo lo scorrimento continuo verso Ovest del cielo serale e vedremo passare più in alto le costellazioni tipiche di ogni stagione. Arrivati al punto iniziale lo scorrimento del cielo serale verso Ovest sarà esattamente di una rotazione completa corrispondente a 24 ore siderali.
Con l’orologio siderale si può specificare la nostra longitudine (es. Forlì 12° Est), la data (es. 4 luglio) e l’ora (es. 23 ora legale) trasformandole in tempo siderale locale (otterremo così 16 e 40). Poi basta mettere a punto il globo sulle 16 e 40 ed ecco l’aspetto del cielo stellato in quel momento con le costellazioni al loro posto. Essendo il 4 luglio alle ore 23 (ora legale) più in alto avremo le costellazioni estive.
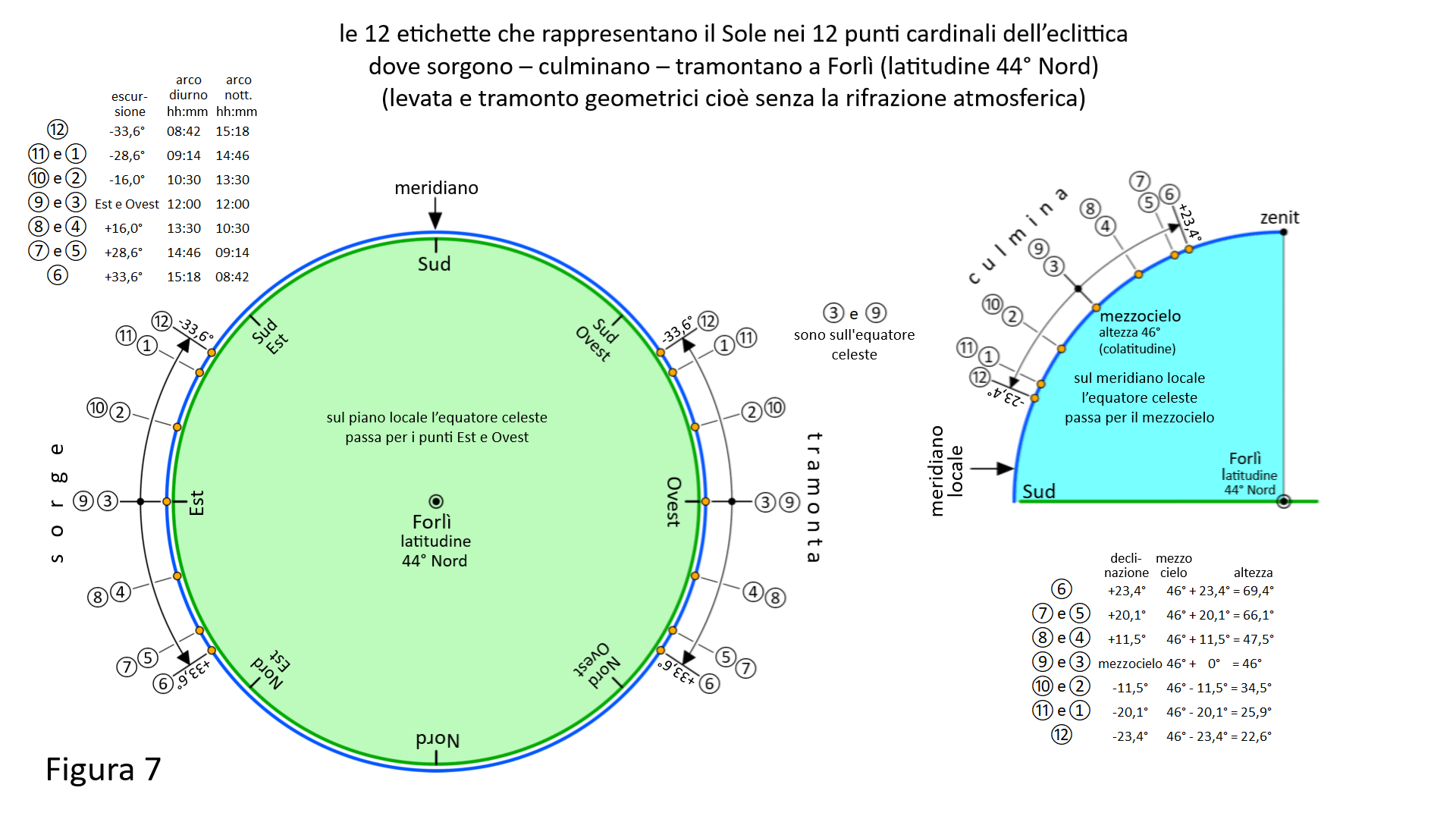
Nella Figura 7 vediamo dove sorge culmina e tramonta il Sole a Forlì (latitudine arrotondata a 44° Nord). A sinistra il cerchio verde rappresenta il piano locale di Forlì (la parte interna al globo) con i punti cardinali, mentre il cerchio blu è la sezione del globo celeste. A destra abbiamo la sezione Sud della sfera celeste con l’arco meridiano blu. L’equatore celeste è inclinato di 46° (colatitudine) sul piano locale; sale a Est, culmina al meridiano sul mezzocielo e scende a Ovest. La rotazione del globo fa fare questo percorso alle etichette ③ e ⑨ che sono sull’equatore celeste. Le altre etichette percorrono cerchi paralleli all’equatore celeste alla distanza angolare della loro declinazione. Sul meridiano la ⑥ ha la massima escursione verso lo zenit +23,4°, mentre la ⑫ ha la massima escursione verso il piano locale a Sud di -23,4°. Sull’orizzonte sia a Est che a Ovest dove l’equatore celeste è inclinato di 46° l’escursione è più ampia arrivando a +33,6° verso Nord per la ⑥ e -33,6° verso Sud per la ⑫.
Nella tabella in alto a sinistra abbiamo le 12 etichette nell’ordine da Sud a Nord in cui sorgono e tramontano centrata sui punti cardinali Est e Ovest. In corrispondenza abbiamo l’escursione in gradi da Est e Ovest, il tempo in ore e minuti dell’arco diurno e dell’arco notturno. L’arco diurno della ⑥ dura ben 15 ore e 18 min, mentre quello della ⑫ solo 8 ore e 42 min. Questi tempi si possono determinare anche con il globo celeste leggendo il tempo siderale alla levata e al tramonto del Sole, facendo poi la differenza (ovviamente non con la precisione del calcolo). Tempo siderale e tempo solare in questo caso si equivalgono per il fatto che il Sole, rappresentato dall’etichetta di turno, sul globo è fermo come il punto gamma.
Il globo celeste riproduce la levata e il tramonto geometrici (con il Sole nella sua direzione reale). Non riproduce ovviamente l’effetto distorsivo della rifrazione atmosferica che solleva leggermente l’immagine del disco solare quando è vicino all’orizzonte: 1,5mm (circa un diametro solare) all’altezza di 0°; 0,4mm all’altezza di 10°; 0,1mm all’altezza di 20°. Nell’ambito di questo modello 1,5mm è comunque poca cosa considerando sempre che la sezione di uno stuzzicadenti è Ø 2mm.
Nella tabella in basso a destra abbiamo le 12 etichette nell’ordine dall’alto al basso in cui passano al meridiano. Sono centrate sul mezzocielo, dove l’equatore celeste interseca il meridiano, altezza 46°. Per ogni etichetta aggiungendo la propria declinazione a 46° otteniamo l’altezza alla quale culmina al meridiano. Abbiamo la ⑥ che passa altissima a 69,4° e la ⑫ che passa molto bassa a 22,6°.
Per spostarci all’equatore (latitudine 0°) dobbiamo ruotare l’anello fino a portare la tacca degli 0° della latitudine Nord di fronte alla lancetta della latitudine Nord. L’asse di rotazione è così disteso sul piano locale nella direzione Nord-Sud. Dall’altra parte la lancetta della latitudine Sud indicherà anch’essa gli 0° della latitudine Sud. Sul meridiano il mezzocielo è salito allo zenit. L’equatore celeste è perpendicolare al piano locale; sale a Est, culmina allo zenit e mezzocielo, scende a Ovest. La ③ e la ⑨ girano sull’equatore celeste (Est – zenit e mezzocielo – Ovest), mentre le altre etichette girano su cerchi paralleli all’equatore celeste e perpendicolari al piano locale, la ⑥ è spostata di 23,4° verso Nord e la ⑫ è spostata di 23,4° verso Sud. A Est e a Ovest passano esattamente come al meridiano. Gli archi diurni sono sempre di 180° così come sono sempre di 180° gli archi notturni: 12 ore di giorno e 12 ore di notte per tutto l’anno. Siccome la levata e il tramonto avvengono perpendicolarmente al piano locale i crepuscoli sono più brevi.
Per spostarci al Polo Nord (latitudine +90°) dobbiamo ruotare l’anello fino a portare la tacca dei +90° della latitudine Nord di fronte alla lancetta della latitudine Nord. L’asse di rotazione è così perpendicolare al piano locale e il Polo Nord celeste è allo zenit. Il mezzocielo è sul piano locale a Sud. L’equatore celeste è disteso sul piano locale e quindi la ③ e la ⑨ girano esattamente sul piano locale sempre pari all’orizzonte. Dalla ③ alla ⑨ girano sempre sopra al piano locale, la ⑥ a +23,4°, e così abbiamo 6 mesi di giorno; dalla ⑨ alla ③ girano sempre sotto al piano locale, la ⑫ a -23,4°, e così abbiamo 6 mesi di notte. Siccome la salita e la discesa del Sole sono molto lente i crepuscoli durano settimane.
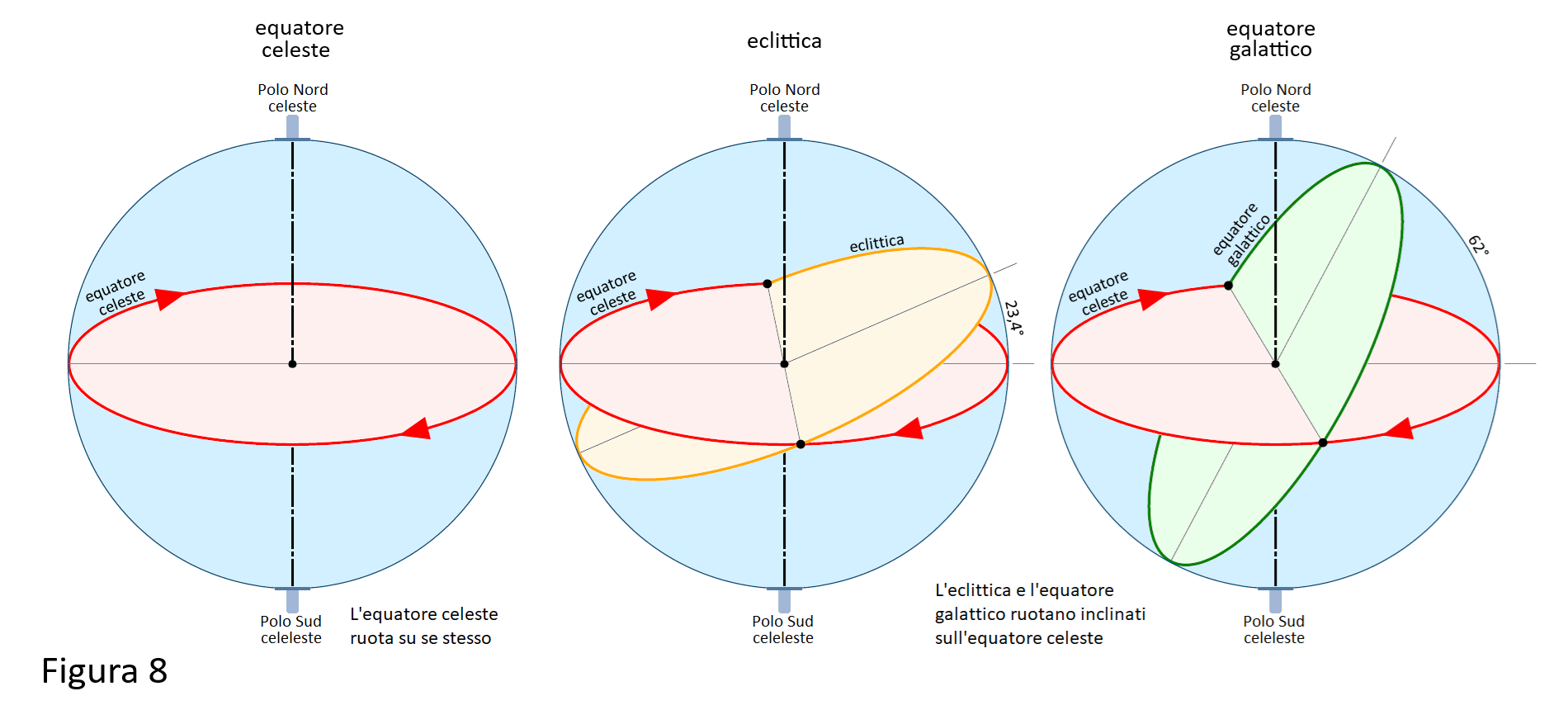
Torniamo alla nostra latitudine media dell’emisfero Nord. Nella Figura 8 abbiamo i 3 cerchi massimi della sfera celeste: l’equatore celeste, l’eclittica, l’equatore galattico. L’equatore celeste è perpendicolare all’asse di rotazione e gira su sé stesso senza oscillare. L’eclittica è inclinata di 23,4° rispetto all’equatore celeste e quindi ha un’oscillazione da +23,4° a -23,4°. Nella Figura 9 vediamo come è disposta l’eclittica rispetto all’equatore celeste nelle ore serali delle 4 stagioni: dalle ore 24 solari di inizio stagione alle ore 18 solari di fine stagione. Il globo celeste riproduce perfettamente questa oscillazione dell’eclittica rispetto sia all’equatore celeste che al nostro piano locale.
Sempre nella Figura 8 abbiamo anche l’equatore galattico come riferimento preciso della via lattea. È inclinato di 62° rispetto all’equatore celeste e quindi ha un’oscillazione molto ampia da +62° a -62°.
La Tabella 2 riporta i passaggi particolari della disposizione della via lattea rispetto al nostro piano locale. La data è al centro di un periodo grosso modo di una ventina di giorni nel quale intorno alle ore 22 solari o 23 legali la disposizione della via lattea è quella descritta nell’ultima colonna. Questi passaggi particolari, che curiosamente hanno una cadenza bimestrale, ci fanno capire che la via lattea è molto movimentata. Come per l’eclittica il globo celeste riproduce perfettamente l’oscillazione della via lattea sia rispetto all’equatore celeste che soprattutto al nostro piano locale.
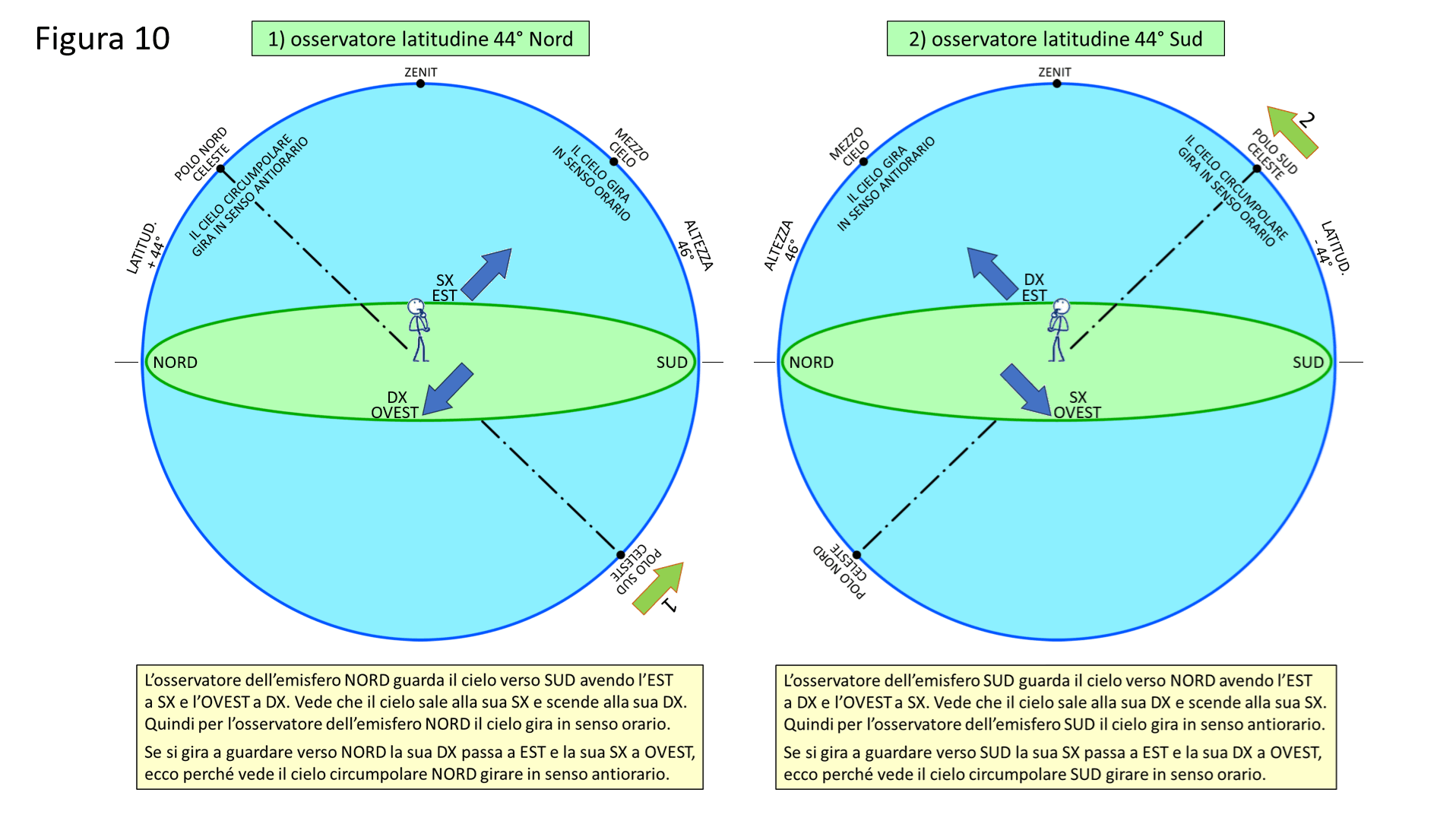
Nella Figura 10 metto a confronto un osservatore di Forlì, latitudine +44° (Nord) con un osservatore della stessa latitudine di Forlì, ma dell’emisfero Sud, latitudine -44° (Sud). Nell’emisfero Sud non c’è molto alla latitudine di 44°: il Sud della Nuova Zelanda e una striscia dell’Argentina e del Cile. Andava bene anche un osservatore di media latitudine Nord e un osservatore di media latitudine Sud.
A sinistra c’è l’osservatore di Forlì. A destra per portarci alla latitudine Sud di -44° dobbiamo portare il Polo Sud celeste 44° sopra il piano locale dalla parte Sud.
L’osservatore di Forlì ha il mezzocielo a Sud, l’Est a sinistra e l’Ovest a destra, e vede il cielo ruotare in senso orario.
L’osservatore del Sud della Nuova Zelanda ha il mezzocielo a Nord, l’Est a destra e l’Ovest a sinistra, e vede il cielo ruotare in senso antiorario.
Il cielo ruota sempre da Est verso Ovest, ma per gli osservatori il senso di rotazione del cielo dipende da come sono girati. Infatti se si girano a guardare il cielo circumpolare si accorgono che gira in senso opposto a quello che guardano normalmente.
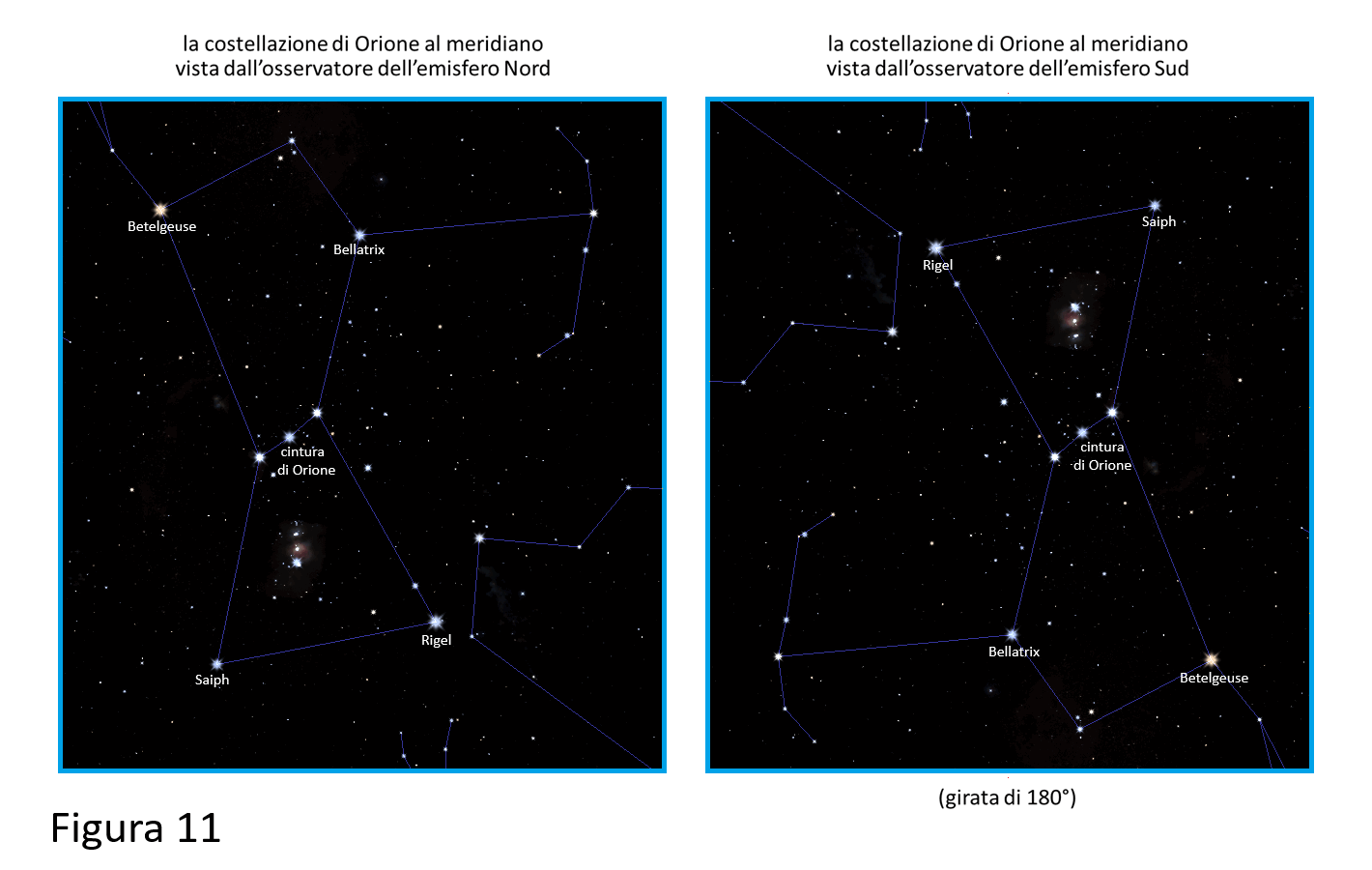
Un’ultima curiosità, prendiamo la costellazione di Orione, che somiglia ad una caffettiera, al meridiano. A sinistra vista dall’emisfero Nord e a destra vista dall’emisfero Sud. Dall’emisfero Sud la si vede girata di 180°. Nella Figura 11 ho utilizzato una schermata di Stellarium che rende meglio l’idea.